不用递归实现用堆栈实现。
先来画个二叉树遍历图:
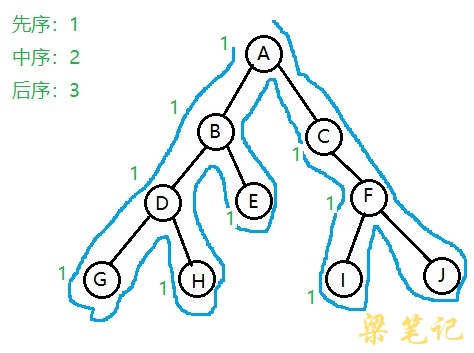
先序、中序、后序遍历二叉树路径都一样,差别是第1次访问到元素先序,第2次访问到元素中序,第3次访问到元素后序。
以中序堆栈实现说明算法:
遇到一个结点,压栈,并去遍历它的左子树
当左子树遍历结束后,从栈顶弹出这个结点并访问它
然后按其右指针再去中序遍历该结点的右子树
|
1 2 3 4 5 6 |
typedef struct TreeNode* BinTree; struct TreeNode{ ElementType Data; BinTree Left; BinTree Right; }; |
下面写出先序,中序、后序非递归代码:
具体Stack堆栈结构部份,请转到这篇:用数组实现栈数据结构 ?? 链式存储如何实现堆栈
先序遍历
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
void PreOrderTraversal(BinTree BT) { BinTree T = BT; Stack S = CreatStack(MaxSize); //创建并初始化堆栈 while(T || !IsEmpty(s)) { while(T){ printf("%d",T->Data); //访问结点 Push(S,T); //压栈 T = T->Left; } if(!IsEmpty(S)){ T = Pop(S); //弹出 T = T->Right; } } } |
中序遍历
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
void InOrderTraversal(BinTree BT) { BinTree T = BT; Stack S = CreatStack(MaxSize); //创建并初始化堆栈 while(T || !IsEmpty(s)) { while(T){ Push(S,T); //压栈 T = T->Left; } if(!IsEmpty(S)){ T = Pop(S); //弹出 printf("%d",T->Data); //访问结点 T = T->Right; } } } |
后序遍历
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
void PostOrderTraversal(BinTree BT) { if(BT == NULL) return ; Stack S = CreatStack(MAX_SIZE); //创建并初始化栈 BinTree Prev = NULL , Curr = NULL; //初始化 s.push(BT); while(!IsEmpty(S)) { Curr = Top(S); //将栈顶元素赋给Curr if(Prev == NULL || Prev->Left == Curr || Prev->Right == Curr) //若Prev为NULL或是Curr的父节点 { if(Curr->Left != NULL) Push(S, Curr->Left); else if(Curr->Right != NULL) Push(S, Curr->Right); } else if(Curr->Left == Prev) //若Prev是Curr的左儿子 { if(Curr->Right != NULL) Push(S, Curr->Right); } else { printf("%d\n", Curr->Data); //访问当前节点 Pop(S); //访问后弹出 } Prev = Curr; //处理完当前节点后将Curr节点变为Prev节点 } } |