图是用来表示“多对多”关系的,现实中有很多这样的关系,如社交网络、村村通公路、交通、线路、结构、流程等等。这些都可以将它规为图。
图在计算机中也是一种数据结构,之前学的树、线性表都是特殊的图。图是“多对多”关系,树是“一对多”关系,线性表是“一对一”关系。
图的定义:
图是一种复杂的非线性数据结构。图在各个领域都有着广泛的应用。图G的二元组定义为:G=(V,E),其中V是顶点集合,即V={vi|0≤i≤n-1,n≥0,vi∈VertexType},VertexType为顶点值的类型,n为顶点数,当n=0时V为空集;E是V上的一个二元关系,即V上顶点的序偶或元序对[每个无序对(x,y)是两个对称序偶<x,y>和<y,x>的简写形式]的集合。对于V上的每个顶点,有E中都允许有任意多个前驱和任意多个后继,即在图中对每个顶点的前驱和后继个数均不加限制。
对于一个图G,若E是序偶的集合,则每个序偶对应图形中的一条向边,若E是元序对的集合,则每个元序对对应图形中的一条无向边,所以可把E看作边的集合。这样图的二元组定义可叙述为:图由顶点集和边集组成。针对图G,顶点集和边集可分别记为V(G)和E(G)。若顶点集为空,则边集必然为空,若顶点集非空,则边集可以为空,也可以不为空,当为空时,图G中的顶点均为孤立顶点。
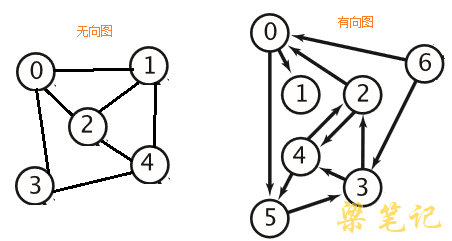
对于一个图G,若边集E(G)中为有向边,则称此图为有向图(directed graph),若边集E(G)中为无向边,则称此图为无向图(undirected graph)。